STRESSES in a THIN CYLINDER subject to INTERNAL PRESSURE - Essay Example

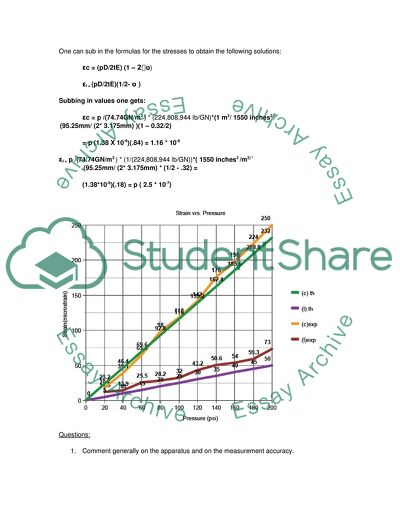
We will examine how far our experimental thin cylinder strays from the ideal linear elastic isotropic we are assuming. We will do this by graphing experimental results versus theoretical calculations. We will take into account the error of the measuring system. We will also investigate the role gauge factor, Young’s Modulus, and Poisson’s ratio play in the effects on strain with pressure. Finally, we will project the outcome of the experiment on the cylinder as the pressure increases to some unknown large finite threshold.

If one were to think of this as in a cylindrical coordinate system, the longitudinal strain would be that acting in the Z direction whereas the cirucumferential (otherwise known as the tangential or lateral) strain would be acting in the direction of theta and not radially. both ends eliminating any longitudinal stress or strain. Our case consists of the second case of a thin cylinder with closed ends. In a thin cylinder with closed ends, longitudinal stresses and strains exist, and both circumferential and longitudinal strains depend on both stresses respectively.

The use of a hand pump allows one to make step measurements of strain at each increment of pressure provided by the hand pump. Each step measurement has a corresponding data point in the table of results. A bourdon gauge is used because it has a tube you can insert inside the cylinder that has the capacity to expand with increasing pressure. The gauge measures the change in its own resistance delta R, and this delta R measured is directly proportional to the respective strain as well as the original resistance R.

The gauge factor is a constant of proportionality between the strain and R, and delta R. The gauge factor of 2.06 is a very typical value for gauge factors. Annealed aluminium is a somewhat ductile or soft metal. Using annealed aluminium is responsible for a somewhat low value of the Young’s modulus. The Young’s modulus of a