Making Connections in Mathematical Learning - Report Example

Making connections in mathematical learning Discuss why children need to learn mathematics in a range of contexts and provide illustrative examples that demonstrate that you clearly understand the link. The earlier Curriculum Guidance for the Foundation Stage document is replaced by the EYFS because “the government believes that improving a child’s development at an early age is essential in improving educational standards later in their lives.“ () It is now legally binding since September 2008 and is separate from the National Curriculum (though it provides the basis for leading onto Key Stage 1). One of the identified areas of learning and development is Problem Solving, Reasoning and Numeracy, which involves learning Mathematics. In addition, the Three Little Pigs story touches upon two other areas such as Creative Development, Communication, Language and Literacy, and Knowledge and Understanding of the World. During the stage of 30-50 months, “literacy and numeracy can develop rapidly with the support of a wide range of interesting materials and activities.” (DCSF Standards) With this in mind, The Three Little Pigs story seeks to stimulate children at this stage in order to make the development of literacy and numeracy skills more effective. Moreover, this story is a good example of material that contains core concepts, which not only connect different areas of Mathematics but also link well with other subjects. This makes it useful for both reinforcing concepts and cross-curricular integration. 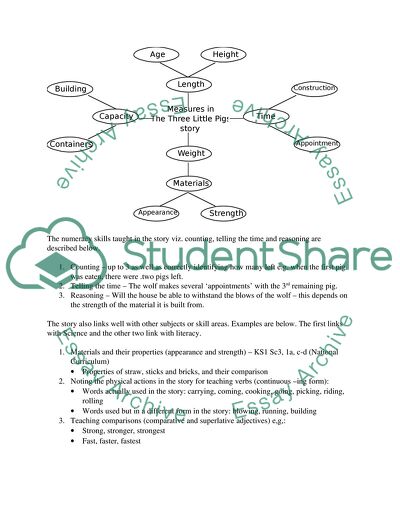The list below enumerates the various numeracy concepts identified in the reading of the story of The Three Little Pigs. They all relate to the central concept of measures and are forms of it. Length Growth in size (the three little pigs grew too big to live with their mother any longer) Height of chimney of the third pig’s house Weight Comparative weights of straw, sticks and bricks Time Time taken for construction (the house of bricks took longer to build) ‘Appointment times’ that the wolf makes with the third pig and the earlier times when the third pig carries out what was asked on his own. Capacity Size of house able to accommodate each pig Capacity of basket which the third pig fills with turnips Size of butter churn Capacity of the pot of water the third pig boils – big enough to hold the wolf A concept map showing the links between different concepts is shown below. The numeracy skills taught in the story viz. counting, telling the time and reasoning are described below. 1. Counting – up to 3 as well as correctly identifying how many left e.g. when the first pig was eaten, there were .two pigs left. 2. Telling the time – The wolf makes several ‘appointments’ with the 3rd remaining pig. 3. Reasoning – Will the house be able to withstand the blows of the wolf – this depends on the strength of the material it is built from. The story also links well with other subjects or skill areas. Examples are below. The first links with Science and the other two link with literacy. 1. Materials and their properties (appearance and strength) – KS1 Sc3, 1a, c-d (National Curriculum) Properties of straw, sticks and bricks, and their comparison 2. Noting the physical actions in the story for teaching verbs (continuous –ing form): Words actually used in the story: carrying, coming, cooking, going, picking, riding, rolling Words used but in a different form in the story: blowing, running, building 3. Teaching comparisons (comparative and superlative adjectives) e,g,: Strong, stronger, strongest Fast, faster, fastest The teachers’ own practices, beliefs and knowledge have a bearing on the pupil learning outcomes in the development of numeracy. Case studies of 18 teachers by Mike Askew et al (1997) looked into this relationship and identified three orientations viz. connectionist, transmission and discovery. The first embodies elements of the other two i.e. it addresses “the role of both the teacher and the pupils in lessons.” (Askew, 1997) However, it is characterised distinctly by involving an “awareness of the links between aspects of the mathematics curriculum.” (ibid) It was found clearly “that those teachers with a strong connectionist orientation were more likely to have classes that made greater gains over the two terms than those classes of teachers with strong discovery or transmission orientations.” (ibid) “Highly effective teachers of numeracy themselves had knowledge and awareness of conceptual connections between areas which they taught in the primary mathematics curriculum.” (Askew, 1997) In other words, students learning under the connectionist oriented teachers exhibited greater gains in the development of numeracy. This points out the effectiveness of emphasising the links that bind different aspects of the subject together. The conceptual connections reinforce learning rather than make students learn things separately and leave making the connections themselves to chance. Thus, teachers who themselves are acquainted with these conceptual connections have an edge over other teachers that don’t and they turn out to be highly effective teachers of numeracy. The implications of the issue of making links to form conceptual connections are very significant to Mathematics. Indeed, the subject of Mathematics is founded upon patterns and relationships. Knowing these underlying patterns and relationships and imparting this to students consolidates their learning. Misconceptions and errors are usually a result of failing to make these conceptual links in Mathematical thinking. So the concept is not grasped properly because it stands alone without fitting in with others. A range of contexts allows greater opportunity for making connections. Making conceptual connections are in accord with the way the brain links knowledge together to facilitate its understanding and recall, and thereby its application. Concepts are the basis upon which learning rests. Therefore it is essential that in the early years of childhood education these concepts be clearly established. “The National Council of Teachers of Mathematics and the National Association for the Education of Young Children affirm that high-quality, challenging, and accessible mathematics education for 3- to 6- year old children is a vital foundation for future mathematics learning.” (NAEYC) Amongst the recommendations of these organisations are ensuring the teaching is “compatible with known relationships and sequences of important mathematical ideas” and integration of “mathematics with other activities and other activities with mathematics.” (ibid) These idea or concepts enable the vital understanding at this critical age and integration provides an opportunity to apply the same concepts in other subjects. Also, “in effective programs, teachers make judicious use of a variety of approaches, strategies, and materials to support children’s interest and ability in mathematics.” (ibid) This allows concepts to develop solidly from a range of perspectives and gives an opportunity for students to practice applying mathematical ideas and skills. The concept of weight of different materials in the story for example can easily be extended to investigating the science of materials and their properties, and as show above the opportunities for literacy development are also numerous. References Askew, Brown et al. (1997) Effective Teachers of Numeracy in Primary Schools: Teachers’ Beliefs, Practices and Pupils’ Learning. King’s College, University of London. (Paper presented at British Educational Research Association Annual Conference, Sep. 1997, University of York) DCSF Standards. http://www.standards.dfes.gov.uk/ http://www.standards.dfes.gov.uk/eyfs/site/childdevelopment/index.htm EYFS. (2005) Early Years Foundation Stage: Direction of Travel Paper. December 2005. NAEYC. (2002) Early Childhood Mathematics: Promoting Good Beginnings. Retrieved Apr. 14, 2009 from: http://www.naeyc.org/about/positions/psmath.asp. UK National Curriculum. http://curriculum.qca.org.uk/key-stages-1-and-2/subjects/science/keystage1/sc3-materials-and-their-properties/index.aspx Read More