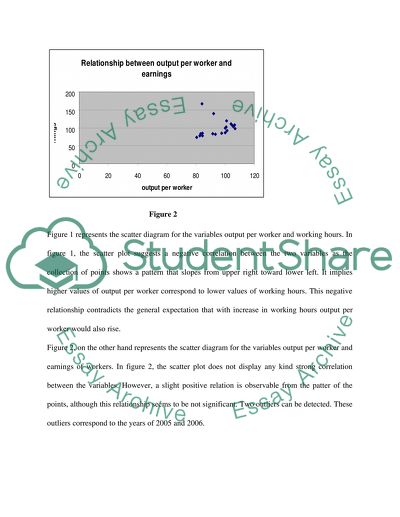
Cite this document
(Relationship between Output Per Worker and Working Hours Statistics Project, n.d.)
Relationship between Output Per Worker and Working Hours Statistics Project. Retrieved from https://studentshare.org/statistics/1553755-undergrad-level-econometricstatistical-analysis
Relationship between Output Per Worker and Working Hours Statistics Project. Retrieved from https://studentshare.org/statistics/1553755-undergrad-level-econometricstatistical-analysis
(Relationship Between Output Per Worker and Working Hours Statistics Project)
Relationship Between Output Per Worker and Working Hours Statistics Project. https://studentshare.org/statistics/1553755-undergrad-level-econometricstatistical-analysis.
Relationship Between Output Per Worker and Working Hours Statistics Project. https://studentshare.org/statistics/1553755-undergrad-level-econometricstatistical-analysis.
“Relationship Between Output Per Worker and Working Hours Statistics Project”. https://studentshare.org/statistics/1553755-undergrad-level-econometricstatistical-analysis.