Vibration - Assignment Example

VIBRATIONS Introduction The stability condition of a two-degree-of-freedom system is represented in physical constants terms of the system; the two-degree-of-freedom system discussed is subjected to self-exciting (Cleghorn, 2010). The solutions of the frequency transfer function might be availed via the substitutions in places of s after obtaining a general transfer function for a system. The two-degree-of-freedom system’s response computation can be also calculated via the Laplace transform (Kelly, 1996). System’s associated vibration modes are calculated using the eigenvectors, which is through the formation of an Eigen vibration problem (Guzzella and Onder, 2010). 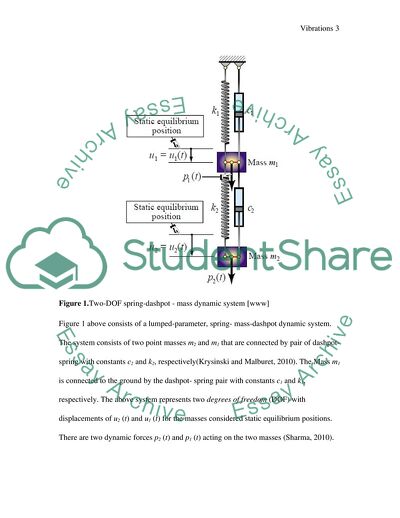Two-DOF Spring-Dashpot - Mass Dynamic System Figure 1.Two-DOF spring-dashpot - mass dynamic system (ASEN, 2013) Figure 1 above consists of a lumped-parameter, spring- mass-dashpot dynamic system. The system consists of two point masses m2 and m1 that are connected by pair of dashpot- spring with constants c2 and k2, respectively(Krysinski and Malburet, 2010). The Mass m1 is connected to the ground by the dashpot- spring pair with constants c1 and k1, respectively. The above system represents two degrees of freedom (DOF) with displacements of u2 (t) and u1 (t) for the masses considered static equilibrium positions. There are two dynamic forces p2 (t) and p1 (t) acting on the two masses (Sharma, 2010). Figure 2. Free body diagram showing EOM (ASEN, 2013) The equations of motion (the EOM) are derived as shown in figure 2. Dashpot and spring forces are indicated by Fdi and Fsi for the ith dashpot and ith spring, respectively; hence the inertia force on the ith mass is given by FIi (Schmitz and Smith, 2012). Figure 3. The positive force convention (ASEN, 2013) Figure 3 shows positive force conventions that are summed along x in order to achieve two force equilibrium equations (Meriam and Kraige, 2012). as at mass 2: p2 – Fd2 – Fs2 – FI2 = 0 as at mass 1: p1 + Fd2 + Fs2 – FI1- Fd1– Fs1 = 0 Scalar form for the EOM The expressions for motion-dependent forces are replaced into displacement DOF, which is into their accelerations and velocities: FI 2 = m2 Fs1 = u1 k1 Fd1 = c1 Fs2 = (u2−u1) k2 Fd2 = ( −) c2 FI 1 = m1 The dashpot and spring that connect masses 2 and 1 have to be expressed in relative velocities and displacements (Dukkipati and Srinivas, 2012). p2 – ( −) c2 – (u2−u1) k2 – m2 = 0 p1 + ( −) c2 + (u2−u1) k2 – m1 - c1– u1 k1 = 0 Grouping terms depending on their time derivatives or the DOF in the LHS and then moving other terms to the RHS. The m terms in the LHS has to be positive (Lurie, Enright and Lurie, 2012). m2 + c2 - c2- u1 k2 + u2 k2 = p2 m1 + c2 + c1 – c2 + u1 k1 + u1 k2 – u2 k2 = p1 Matrix Form for the EOM When rewriting the scalar form of the EOM, then: + + = Expressing in the compact matrix notation then; MC + Ku = p Where C, K, and M are the damping, stiffness, and mass respectively, while, , u, and p are acceleration, velocity, displacement, and force respectively (Iyengar, 2010). Eigen Frequency computation Considering the system in figure 1, when m2=1, m1=2, c2=c1=0, k2=3, p2=p1=0, k1=6; while the stiffness and mass matrices are K= M= The dynamic force vector with the damping matrix, that is p and C respectively, will vanish (Norton, 2009). = 2 = After finding the characteristic polynomial equation det= +18-15= (6-)(3-) The equation results into to two undamped natural squared frequencies, that is, =1.5 or =6 The undamped natural frequencies are =2.4 and =1.2 which is equivalent to f2=0.39 Hz and f1=0.2 Hz respectively (Bequette, 2003). Deriving Frequency Transfer Function The frequency transfer functions of x 2(t) and x 1(t) for the system in figure 4 (a) will be derived. Therefore, from the diagrams of the free-body in figure 4 (b), the system’s equations of motion are (Lalanne, 2013) : m2 + ( –)c2 + k2( - )= 0 =p2 (E.1) m1+ k1x1 + c1 + ( –)c2+ k2( - ) = p0 Sin = p1 (E.2) (a) (b) Figure 4. System and free-body diagram (Gross et al., 2014) By applying the Laplace transforms of the equations (E.2) and (E.1), and assuming the zero initial condition, then; m2s2X2(s) + k2[X2(s) - X1(x)] + c2s[X2(s) - X1(s)] = 0 (E.3) m1s2X1(s) + k1X1(s) + c1sX1(s) + k2[X1(s) - X2(s)] + c2s[X1(s) - X2(s)] = P1(s) (E.4) X2(s)= (E.5) X1(s)= (E.6) D2(s) = (k2 + c2s)P1(s) (E.7) D1(s) = (m2s2 + k2 + c2s)P1(s) (E.8) D(s) = (m1m2)s4 + [m1c2 + m2c2+ m2c1]s3 + [m1k2 + m2k2+ m2k1 +c1c2]s2 + [c2k1 + c1k2]s + (k1k2) (E.9) Equations (E.7) to (E.9), transfer functions of x2(t) and x1(t) are obtained from (E.6) and (E.6) as follows: = (E.10) = (E.11) D(s) is obtained from equation (E.9); when setting s=i in the equations (E.9), (E.10), and (E.11), then the transfer functions of x2(t) and x1(t) are obtained as: = (E.12) = (E.13) and D(i) = 4(m1m2)4 - 2 [m1k2 + m2k1 + m2k2 + c1c2] - i3[m1c2 + m2 c1 + m2 c2] + i [c1k2 + c2k1] +(k1k2) Equation 14 Finding the Steady-State Response for the System By neglecting damping, that is setting c2=c1=0; the frequency transfer function is obtained from (E.13) and (E.12) as follows (Reynolds, 2013): T2() = = (E.1) T1() = = (E.2) Therefore; = Equation 3 The steady-state solution for x1(t) is achieved using p0 Sin =po = || Sin = Sin ( +) Equation 4 Given that == or 0 Equation 5 Using equations (E.4) and (E.4), x2(t) is obtained as: = || Sin ( +)=|| || Sin ( +) Therefore = Sin ( +) = Sin (+) Equation 6 And == or 0 Conclusion From the equations, using figure 4, or are either or 0. When assuming that m2 and m1 move in phase with, then (0); and when out of phase is equal to (Kelly, 2012). Masses m2 and m1 move in same direction, given that , and they will consequently move in the opposite direction given that . And finally, if , m2 turns into a sinusoidal motion while m1 will experience no movements (Bhavikatti and Rajashekarappa, 2008). For easy calculations of Eigen values, MatLAB should be utilized, in order to guarantee accuracy, and system adjustments towards stability; MatLAB also provides frequency maps, thus avails detailed information of the system. . References ASEN, 2013. University of Colorado Boulder. [Online] Available at: www.colorado.edu%2Fengineering%2FCAS%2Fcourses.d%2FStructures.d%2FIAST.Lect19.d%2FIAST.Lect19.Slides.pdf&ei=L6kIVZLaFY-JuwSn9YHwAQ&usg=AFQjCNFNZo [Accessed 18 March 2015]. Bequette, B. (2003). Process control. Upper Saddle River, N.J.: Prentice Hall PTR. Bhavikatti, S. and Rajashekarappa, K. (2008). Engineering mechanics. New Delhi: New Age International (P) Ltd. Cleghorn, W. (2010). Mechanics of machines. New York: Oxford University Press. Dukkipati, R. and Srinivas, J. (2012). Textbook of mechanical vibrations. New Delhi: PHI Learning. Geradin, M. and Rixen, D. (2015). Mechanical Vibrations. Chichester: Wiley. Gross, D., Hauger, W., Schröder, J., Wall, W. and Govindjee, S. (2014). Engineering Mechanics 3. Berlin, Heidelberg: Springer. Guzzella, L. and Onder, C. (2010). Introduction to control and modeling of systems. Berlin: Springer. Iyengar, R. (2010). Elements of mechanical vibration. New Delhi: Indian International Publishing House Pvt. Limited. Kelly, S. (1996). Schaums outline series on mechanical vibrations. New York: McGraw-Hill. Kelly, S. (2012). Mechanical vibrations. Australia: Cengage Learning. Krysinski, T. and Malburet, F. (2010). Mechanical Vibrations. Hoboken: John Wiley & Sons. Lalanne, C. (2013). The Mechanical Vibration and Shock Analysis. New York, NY: John Wiley & Sons. Lurie, B., Enright, P. and Lurie, B. (2012). Classical feedback control with MATLAB and Simulink. Boca Raton, FL: CRC Press. Meriam, J. and Kraige, L. (2008). Engineering mechanics. New York: J. Wiley. Meriam, J. and Kraige, L. (2012). Engineering mechanics. Hoboken, NJ: Wiley. Mostafa, M. (2013). Mechanics of machinery. Boca Raton, FL: CRC Press. Norton, R. (2009). Kinematics and dynamics of machinery. Boston, Mass.: McGraw-Hill. Reynolds, D. (2013). Engineering principles of mechanical vibration. [S.l.]: Trafford On Demand Pub. Schmitz, T. and Smith, K. (2012). Mechanical vibrations. New York: Springer. Sharma, D. (2010). Engineering mechanics. New Delhi: Dorling Kindersley. Wang, L. (2009). The model predictive control system designing with implementation utilizing MATLAB®. London: Springer. Read More