Body Mass Index of Females in the US - Assignment Example

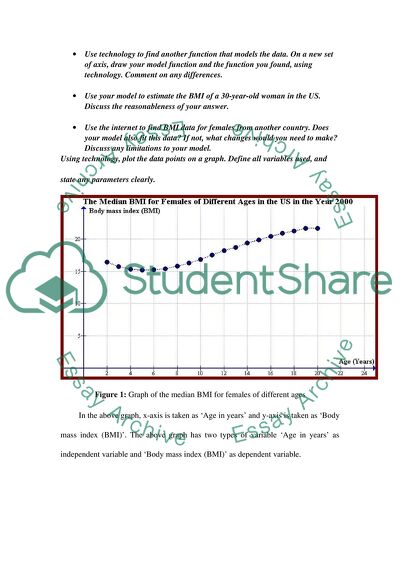
Math work Faculty BODY MASS INDEX SL TYPE II Body mass index (BMI) is a measure of one’s body fat. It is calculated by taking one’s weight (kg) and dividing by the square of one’s height (m). The table below gives the median BMI for females of different ages in the US in the year 2000. Age (yrs) BMI 2 16.40 3 15.70 4 15.30 5 15.20 6 15.21 7 15.40 8 15.80 9 16.30 10 16.80 11 17.50 12 18.18 13 18.70 14 19.36 15 19.88 16 20.40 17 20.85 18 21.22 19 21.60 20 21.65 Using technology, plot the data points on a graph. Define all variables used, and state any parameters clearly. What type of function models the behavior of the graph? Explain why you chose this function. Create an equation (a model) that fits the graph. On a new set of axes, draw your model function and the original graph. Comment on any differences. Refine your model if necessary. Use technology to find another function that models the data. On a new set of axis, draw your model function and the function you found, using technology. Comment on any differences. Use your model to estimate the BMI of a 30-year-old woman in the US. Discuss the reasonableness of your answer. Use the internet to find BMI data for females from another country. Does your model also fit this data? If not, what changes would you need to make? Discuss any limitations to your model. Using technology, plot the data points on a graph. Define all variables used, and state any parameters clearly. Figure 1: Graph of the median BMI for females of different ages In the above graph, x-axis is taken as ‘Age in years’ and y-axis is taken as ‘Body mass index (BMI)’. The above graph has two types of variable ‘Age in years’ as independent variable and ‘Body mass index (BMI)’ as dependent variable. What type of function models the behavior of the graph? Explain why you chose this function. Create an equation (a model) that fits the graph. The graph of the median BMI for females of different ages in the US in the year 2000 is shown in figure 1. From graph, it can be seen that BMI for females decreases slowly from age 2 to age 5. Thereafter, BMI start increases from age 5 to subsequent years and shows a linear trends. In general, this type of data plots can be modeled accurately using polynomial function of higher order (order 2 and above). However, since here in this case, it can be seen that the data plots shows linear trends, therefore, we will model this data plot using linear function model. Let us assume that the equation of model linear function is: Where, ‘m’ is slope and ‘c’ is intercept of the linear function. Since, there are different data points, therefore, for calculating slope and intercept, we will use below formulas: and The equation will be: Or Correlation Coefficient will be: Coefficient of Determination: The value of Correlation Coefficient (R) of 0.949682 implies that the data are highly positively correlated. The value of Coefficient of Determination () of 0.901896 implies that 90.19% of the BMI can be determined by equation. Age (yrs) (x) BMI (y) 2 -9 81 16.4 -1.57105 2.468206371 14.13947368 3 -8 64 15.7 -2.27105 5.157680055 18.16842105 4 -7 49 15.3 -2.67105 7.134522161 18.69736842 5 -6 36 15.2 -2.77105 7.678732687 16.62631579 6 -5 25 15.21 -2.76105 7.623411634 13.80526316 7 -4 16 15.4 -2.57105 6.610311634 10.28421053 8 -3 9 15.8 -2.17105 4.713469529 6.513157895 9 -2 4 16.3 -1.67105 2.792416898 3.342105263 10 -1 1 16.8 -1.17105 1.371364266 1.171052632 11 0 0 17.5 -0.47105 0.221890582 0 12 1 1 18.18 0.208947 0.043659003 0.208947368 13 2 4 18.7 0.728947 0.531364266 1.457894737 14 3 9 19.36 1.388947 1.929174792 4.166842105 15 4 16 19.88 1.908947 3.644080055 7.635789474 16 5 25 20.4 2.428947 5.899785319 12.14473684 17 6 36 20.85 2.878947 8.28833795 17.27368421 18 7 49 21.22 3.248947 10.555659 22.74263158 19 8 64 21.6 3.628947 13.169259 29.03157895 20 9 81 21.65 3.678947 13.53465374 33.11052632 Average age () = 11 Average BMI () = 17.9710526 On a new set of axes, draw your model function and the original graph. Comment on any differences. Refine your model if necessary. Figure 2: Graph of the median BMI for females of different ages and Model function Figure 2, shows the original graph and graph of the model function. The graph of model function (equation) significantly fit the original graph of the median BMI for females of different ages in the U.S. in the year 2000. The slight difference in the graph of model function is in the age for 2 to 3 years. Use technology to find another function that models the data. On a new set of axis, draw your model function and the function you found, using technology. Comment on any differences. Below polynomial function of order 4 (Quartic function) is found using technology (Microsoft Excel). The value of Coefficient of Determination () of 0.9997 for this quartic function implies that 99.97% of the BMI can be determined by this quartic equation. Figure 3: Graph of Model function and Quartic Function Figure 3 shows the graph of Model function: and Quartic Function:. The main difference between the two models is that model function determines 90.19% of the BMI for the given ages as compared to Quartic Function determines 99.97% of the BMI for the given ages. In other words, it can be said that the Quartic function obtained using technology (Microsoft Excel) models the given data more precisely as compared to derived linear model function. Use your model to estimate the BMI of a 30-year-old woman in the US. Discuss the reasonableness of your answer. Using model function, the BMI for a 30-year-old woman in the US comes out to be 25.66. The answer is reasonable because BMI calculated using model function falls in marginally overweight region for women. However, if we calculate BMI using Quartic Function: , than it comes out to be 19.193, that falls in normal range. However, the BMI calculated here is for the 30-year-old woman and we had modeled the function using 2 to 20 years age of data. Therefore, we cannot be sure that the BMI will be lower or higher for 30-year-old woman than 20-year-old woman. In practical, BMI is always higher for 30-year-old woman than 20-year-old woman. Use the internet to find BMI data for females from another country. Does your model also fit this data? If not, what changes would you need to make? Discuss any limitations to your model. Below tables shows Body mass index (kg/m²) of Guatemalan children, adolescents and young adults.   Females Age (y) Median Birth 13.3 0.25 16.2 0.5 17.0 0.75 16.7 1.0 16.4 1.5 16.0 2.0 16.0 2.5 16.0 3.0 15.9 3.5 16.1 4.0 15.8 5.0 15.5 6.0 15.2 7.0 15.2 11.0-11.9 16.5 12.0-12.9 17.2 13.0-13.9 18.8 14.0-14.9 19.3 15.0-15.9 20.2 16.0-16.9 21.6 17.0-17.9 21.8 18.0-24.9 21.8 The model function derived earlier also fit above table data. The main limitation of the model function is that is derived using a very small sample/population of data. In addition, the data given is also for the 2 to 20 years range. Therefore, it is not practically feasible to predict BMI for adults women using model function derived from this limited set of data. References: http://www.halls.md/body-mass-index/overweight.htm accessed on May 25, 2008 http://www.unu.edu/unupress/food2/uid02e/uid02e0e.htm accessed on May 25, 2008 Appendix 1: BMI for Women The "National Average" Median Body Mass Index values for Women are: Age: 20-29 yrs 30-39 yrs 40-49 yrs 50-59 yrs 60-69 yrs Median BMI: 24.4 26.4 27.8 28.4 27.5 Adults Women Men underweight 31.1 Read More