Quantitative Methods for Finance:Dynamic Regression - Report Example

Capital Asset Pricing Model (CAPM Data Plots The exercise focuses on two stocks ly IBM (Computers) and Citicorp (Banks). The plots focus on the 5-year period between January 1983 and December 1987 and are shown below: The plot for Citicorp shows that the returns are in the range of [-0.3, 0.15] and have been fluctuating between positive and negative values throughout the sample period. The returns for IBM also exhibit similar behaviour with the range [-0.2, 0.15]. However, it appears that the drop in return for the IBM stock in the aftermath of the market crash of October 1987 were less severe than the drop experienced by Citicorp indicating that the computing industry was less affected by the market crash in comparison to the banking sector. 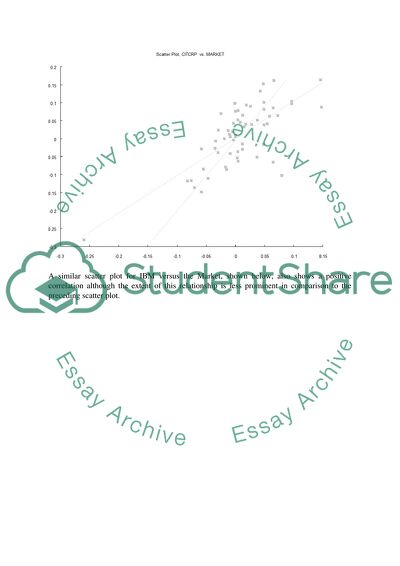The scatter plot of the returns of Citicorp against the market is shown below indicating a positive correlation between both the series. A similar scatter plot for IBM versus the Market, shown below, also shows a positive correlation although the extent of this relationship is less prominent in comparison to the preceding scatter plot. 2. Ordinary Least Squares Estimation for α and β. The OLS results for Citicorp are listed below: The values from the above results are, α = 0.00099 and β = 1.0394. The 95% confidence intervals for the parameters are based on the formula: Mean ± (1.96)*SD/Sqrt(n), where SD is the standard deviation and n is the sample size. Thus the confidence intervals for the parameter ‘Market’ are given as: 1.0394 ± (1.96 * 0.1118)/Sqrt(60) = 1.0394 ± 0.0283 = {1.011, 1.067} Similarly, the confidence intervals for the parameter ‘intercept’ or ‘α’ are: 0.00099 ± (1.96 * 0.00727)/Sqrt(60) = 0.00099 ± 0.0018 = {-0.00081, 0.00279} The OLS results for IBM are shown below: 3. Residual SD and R-Squared estimates The Residual SD measures the individual risk of the stock and is 0.0585 for Citicorp and 0.0472 for IBM. The Residual SD is a measure of the SD of points generated using a linear function and gives an indication of the dependent variable’s accuracy. The low values for SD in both cases indicate a higher degree of accuracy in the estimation. The R-Squared value indicates the proportion of risk that is attributable to market-driven factors and is 0.5347 for Citicorp and 0.413 for IBM. This means that 53.47% of the total variation in the Citicorp stock can be explained by the market while only 41.3% of the variation in the IBM stock is accounted for by the market. Thus, Citicorp is more influenced by market conditions in comparison to IBM which also explains the higher drop in the former during the market crash of October 1987. 4. Verifying the CAPM The summary statistics for the two variables in the case of Citicorp are shown below: The value of β for Citicorp is calculated using the CAPM equation (eqn, 2) provided in the instructions. β (Citicorp) = (0.01 – 0.00559)/(0.0087 – 0.00559) = 0.00441/0.00311 = 1.41 β (Citicorp) calculated above is higher than the estimate calculated through the OLS method. β (Citicorp) = 1.41 while β (Citicorp/OLS) = 1.0394 Summary statistics for IBM are shown below: Using a similar approach, β (IBM) = (0.0076 – 0.00559)/(0.0087 – 0.00559) = 0.00201/0.00311 = 0.646 β (IBM) = 0.646 while β (IBM/OLS) = 0.656 suggesting a close match in the β estimates from both methods. 5. Chow Stability Test The Chow test statistics for Citicorp are shown below: The Chow’s stability test gives a value of 5.6179, which is greater than the critical value of 3.074. This leads to the rejection of the null hypothesis that the CAPM equation for Citicorp is stable over the 10 year sample period. Hence, this leads to the acceptance of the alternate hypothesis that there is no structural stability or that there is a structural change. The results of the Chow stability test for IBM are shown below: The computed F-Statistic under the Chow Stability test is 2.865, which is less than the critical value of 3.074. This leads to the acceptance of the null hypothesis that the model is stable in the case of IBM stock within the 10 year sample period between January 1978 and February 1987. 6. Strict CAPM against the Arbitrage Pricing Model (APM) The variable addition test is computed using an F-test shown by the following formula: .....eq. 1 where, q = 3, the number of new regressors R2new = 0.5752 R2old = 0.5347 n = 60 k = 4, the number of parameters in the new model. F (3, 56) = [(0.5752 – 0.5347)/3]/[(1 - 0.5752)/56] = 0.01283/0.00758 = 1.6926 This value is less than the critical value of 2.769 thereby leading to the acceptance of the null hypothesis that the inclusion of the new variables (GIND, RINF and ROIL) in the regression model does not contribute significantly to the explanation of CITCRP, the dependent variable. The Wald test is used to test the joint significance of a set of coefficients used in the regression. In the case of Citicorp, the F-Statistic for the Wald test is 18.6149, which is much higher than the critical value of 2.5396. Hence, the null hypothesis is rejected to suggest that at least some of the variables constituting the model are significant in comparison to others. The results of the variable addition test for IBM are shown below: Applying the same formula from equation 1, F (3, 56) = [(0.4279 – 0.413)/3]/[(1 – 0.4279)/56] = 0.00496/0.0102 = 0.4862 The F-test for the variable addition also yields a test statistic which is less than the critical value thereby confirming the null hypothesis that the addition of GIND, RINF and ROIL to the linear regression has not affected the estimation of IBM (the dependent variable) in a significant manner. The Wald test for the IBM test also indicates that the test statistic is higher than the critical value thereby rejecting the null hypothesis. This means that removing some variables may influence the fit of the model. The variable addition tests for both the stocks suggest that the inclusion of the macroeconomic variables into the regression model does not increase the chances of predictability in a significant manner. Read More