Patient at Risk of Diabetes at Rushed Hospital - Assignment Example

Patient At risk of diabetes at Rushed Hospital Diabetes is a disease that affects how the body uses blood glucose. Doctors believe that the age of individuals highly influences their probability of getting diabetes. The doctors at Rashid Hospital have taken records of patients at the risk of getting diabetes and aim to use mathematical knowledge to carry out analysis on this data. Aim of the project The purpose of this paper is to apply statistical knowledge to analyse the data of the ages of patients at Rashed Hospital, who are at risk of getting diabetes. Use of mathematical knowledge will help draw conclusion on the prevalent of the risk and the ages at which the risk is highest. Data collection/classes The data on the ages of the patients at risk of getting diabetes is secondary data derived from the Rashed Hospital records. 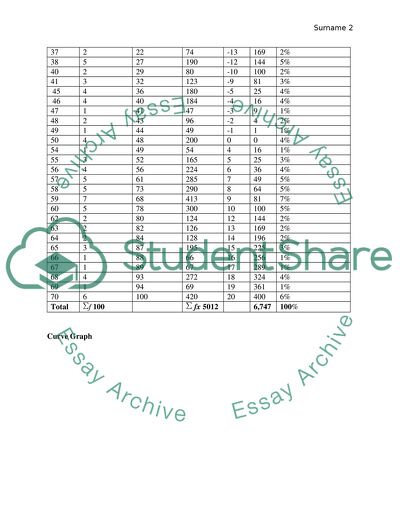Age (x) Frequency(f) Cumulative frequency f*y x-µ (x-µ)2 Probabilities of getting Diabetes 23 2 2 46 -27 729 2% 26 2 4 52 -24 576 2% 27 1 5 27 -23 529 1% 28 2 7 56 -22 484 2% 30 8 15 240 -20 400 8% 32 2 17 64 -18 324 2% 35 2 19 70 -15 225 2% 36 1 20 36 -14 196 1% 37 2 22 74 -13 169 2% 38 5 27 190 -12 144 5% 40 2 29 80 -10 100 2% 41 3 32 123 -9 81 3% 45 4 36 180 -5 25 4% 46 4 40 184 -4 16 4% 47 1 41 47 -3 9 1% 48 2 43 96 -2 4 2% 49 1 44 49 -1 1 1% 50 4 48 200 0 0 4% 54 1 49 54 4 16 1% 55 3 52 165 5 25 3% 56 4 56 224 6 36 4% 57 5 61 285 7 49 5% 58 5 73 290 8 64 5% 59 7 68 413 9 81 7% 60 5 78 300 10 100 5% 62 2 80 124 12 144 2% 63 2 82 126 13 169 2% 64 2 84 128 14 196 2% 65 3 87 195 15 225 3% 66 1 88 66 16 256 1% 67 1 89 67 17 289 1% 68 4 93 272 18 324 4% 69 1 94 69 19 361 1% 70 6 100 420 20 400 6% Total f 100 fx 5012 6,747 100% Curve Graph The chart above shows the risk of getting diabetes based on the age of individuals. From the graph, we can view the rate of the risk at a glance. Example, the rate is highest at age thirty. There is no constant movement causing high variations. Ogive An ogive uses the cumulative frequency and not the normal rate. It is easy to determine data are lying above or below a given point. For example, it is easy to determine all the patients who are below or above the mean age or those above and below the median age. Pie Chart The pie chart below also shows this frequency. Central tendency measures Central tendency measures locate the central position of distribution around which the values of the item of distribution tend to concentrate. It represents the entire series. It helps to compare different distributions. They are also referred to as averages and include arithmetic mean, mode and median. These measures enhance comparison; example compares the ageing population of patients between two or more hospitals. Mean- The mean is the simple average of the data. It is calculated by dividing the sum of the data with the number of variables (Khan 136). We add all the ages of the patients at risk of diabetes in the hospital and divide the total age by the total number of patients (n). Mean (µ) = fx / n =5,012/100 =50.12 years. Approx. 50 years. This means that on average the age of people at risk of getting diabetes is 50 years. Median-it gives the middle value of the distribution (Khan 142). The median age is the age at the middle of all the patient’s ages. It divides the ages into two equal positions. It is gotten by arranging the ages from the lowest to the highest, dividing n by two and getting the value that coincide with n/2. In our case n=100; n/2=50. From the table above, we consider the 50th age distribution. The 50th number is 55 which is hence our median dividing the distribution into two. Mode- this is the value that occurs maximum times in the data (Khan 149). In this case it is the age that is most prevalent, 30 years is the most recurrent occurring eight times and is hence the mode. This means that people aged 30 years are at a higher risk of getting diabetes. Measures of dispersion Standard deviation (σ) - it measures the variability or dispersion from the mean (Khan 171). It shows how much the data is deviating from the expected rate or the mean. In this case, standard deviation shows the deviation of the ages from the mean age of 50 years. σ= sqrt 6,747/100 σ=8.12 this shows that the ages vary highly from the mean. Range- This is the difference between the highest and lowest ages (Khan 161). The oldest person at risk of getting diabetes is 70 years whereas the youngest person is 23 years. The range, therefore, is 70-23=47years. The range is, therefore, 47 years. Probability and skewness Using the probability as provided in the table it is possible for an individual to determine the possibility of getting diabetes on the basis of their age. The probability is highest in people at the age of 30; some like those at age 24,25,29,33,34,42,43,51,52,53 are at 0% risk while others example at age 27,36,47,49,54,69,67, and are at lower risks, that is, their chance of getting diabetes is 1%. Skewness measures the asymmetry of the probability distribution of values about their mean (Khan 174). The mean, mode and median are used to determine the skewness, that is, whether positively or negatively skewed. The mean is 50 is equal to the average, and both are greater than the mode. This implies positive skewness Analysis of the data From the data, it is evident that people at the age of 30 years are at the highest risk of getting diabetes and the age at which people can get diabetes is highly distributed with a very high range of 47 years meaning those who don’t get the disease at their early ages are still at risk even as they grow up. The age of an individual is a major factor in the determination o the possibility of getting diabetes. Conclusion In conclusion it is evident that statistical knowledge is very important in our day to day operations. It is helpful in analyzing data and will help draw conclusions and can be used by managers in decision making. Reference Khan, J. A. Research Methodology. New Delhi: APH Publishing Corporation, 2008. Print. Read More